Distributed Parameter Systems are everywhere.
    Because they are difficult to deal with, engineers generally avoid partial differential equations. They reason that lumped parameter models will generally suffice and in recent years, finite element analysis has provided a real verification of that idea and the tools to work with.  However, there are still some benefits from thinking things through in terms of continuum mechanics.

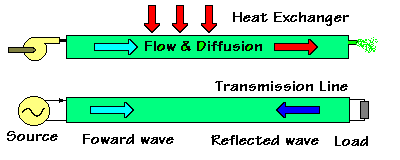
All the physical objects in use are spread out in space.

Distillation columns, heat exchangers, chemical reactors are examples. Making a lumped model approximation is most often quite sufficient, but not always. Sudden shocks that pass though solids or liquids, heat transfer into slabs of material, flow and diffusion processes, all are naturally described by partial differential equations. Knowing the character of those equation systems and how they can be expected to behave is valuable. Sometimes a good approximation to questions of propagation and response can be obtained analytically. Even if the modelling will have to be done as a lumped or finite element job, the partial differential equation basis is a good place to start to define the quantization level and the options for simulation, modelling and control system design. Here are some thoughts from McCann's experience with distributed parameter systems. (This experience goes back to McCann's doctoral thesis and subsequent research. List of publications)

39 Ways to model dynamic distributed parameter systems.
    There are really only thirty nine ways to set up models for dynamic distributed parameter systems. There can be at most 3 space dimensions and a time dimension. Each dimension can be treated by a continous integration, a transform method (e.g. Laplace, Fourier, Bessel) or by discretization. In any one model only one dimension can be treated continuously (e.g by analog computer or its numerical equivalent).
    With one-space systems, the two dimensions give nine (3 by 3) ways but the simultaneous use of continuous integration on two variables is not feasible leaving eight ways for 1-space dynamic systems.
    For two space dimensions, which are, from the point of view of methodology, indistiguishable, out of the 27 starters only 13 remain as distinct when we recognise that time with its one directional nature is different from a space dimension.
    For three space dimensions, the number of distinct options is 18. So the grand total of methods is 39.

Chosing a method.
     Assuming you are not going to jump into finite elements software without thinking about it, then there is a choice of approach. Transform methods eliminate independent variables in favour of algebraic variables. For example a Laplace transform will eliminate an independent variable over the domain 0 to infinity, giving a continuous range of  transformed variable. The usual example is "time" becoming transformed to "frequency" and the system is analysed with frequency as a parameter of a simpler differential equations set (or if you started with a lumped parameter system only algebraic equations remain).
    When the range of the independent variable is finite, the transform method will be a finite transform and yield a discrete valued variable. For example, a finite Fourier transform yields a set of coefficients each of which defines the size of a mode which has a sinusoidal shape.
    Discretization chops the dimension into sectors in which some assumption of uniformity or continuity is made. The simplest is to assume the regions have uniform value of dependent varibles within them.
    The question of which method then becomes one first of feasibility and then of practicality. Only linear systems will work properly with transform methods, but when they do, the resulting simplification can be very powerful leading to solutions of any desired accuracy. Discretization leads to there being many equations to solve. McCann can help you with the choice and the solutions, adapted to the problems you have to solve. (Go to our Index page to find out more)

Elliptic, Parabolic or Hyperbolic Partial Differential Equations.
If you know whether an equation system is elliptic, parabolic or hyperbolic you have already a good idea of its basic behaviour. You also have some pointer as to the best solution methods. Elliptic PDE's give steady state solutions. Relaxation methods work with them in most physical systems which are intrinsically stable. Parabolic PDE's come from systems in which flow and dispersion (diffusion) both occur. McCann has some guidelines for knowing how to chop them up into the minimal number of elements. Hyperbolic equations are for idealised non dissipative propagation. Transmission lines for telecommunications are often thought about this way. McCann has done some work on transmission lines which don't behave like the usual theory, but yet, being linear, yield to transform methods.

Getting help.
    If you have a problem with the behaviour of a distributed parameter system (process) and would like to get a quantitative handle on it to improve yield or optimise performance, then contact McCann Science.

About McSc
Summary
Principal (CV)
Contacting us
Contact in UK
Location USA
Philosophy
Software Tools
Fees
CAD service

Applications

Business & Commerce
TV Advertising
Drugs Competition
Housing Demand
Automobiles Demand
Wallcoverings Battle
Cash Flow
Human Resources
Project Management
Patent Analysis

Chemical Industry
Cooling Tower
Fermentation
Polymer Process
Heat exchange
Supercritical Fluid
Distributed parameter
Toxic gas allocation

Electrical
Control systems
Initiation systems
Ferrite Filters
Microstrip Antennas
Lightning

Production & Process
Automated manufacture
Crimp and Press
Glass making
Glass molding
Glass to metal seals
Heat exchanger
Helium Leak Testing
RF Soldering
Vacuum web coating

Applications.